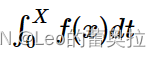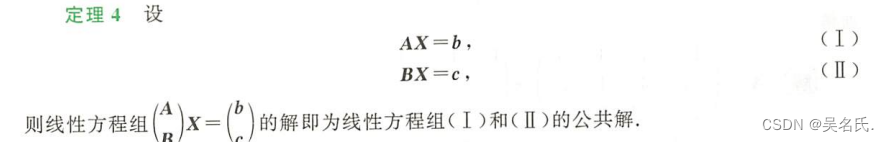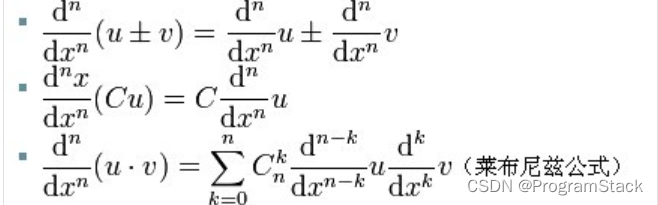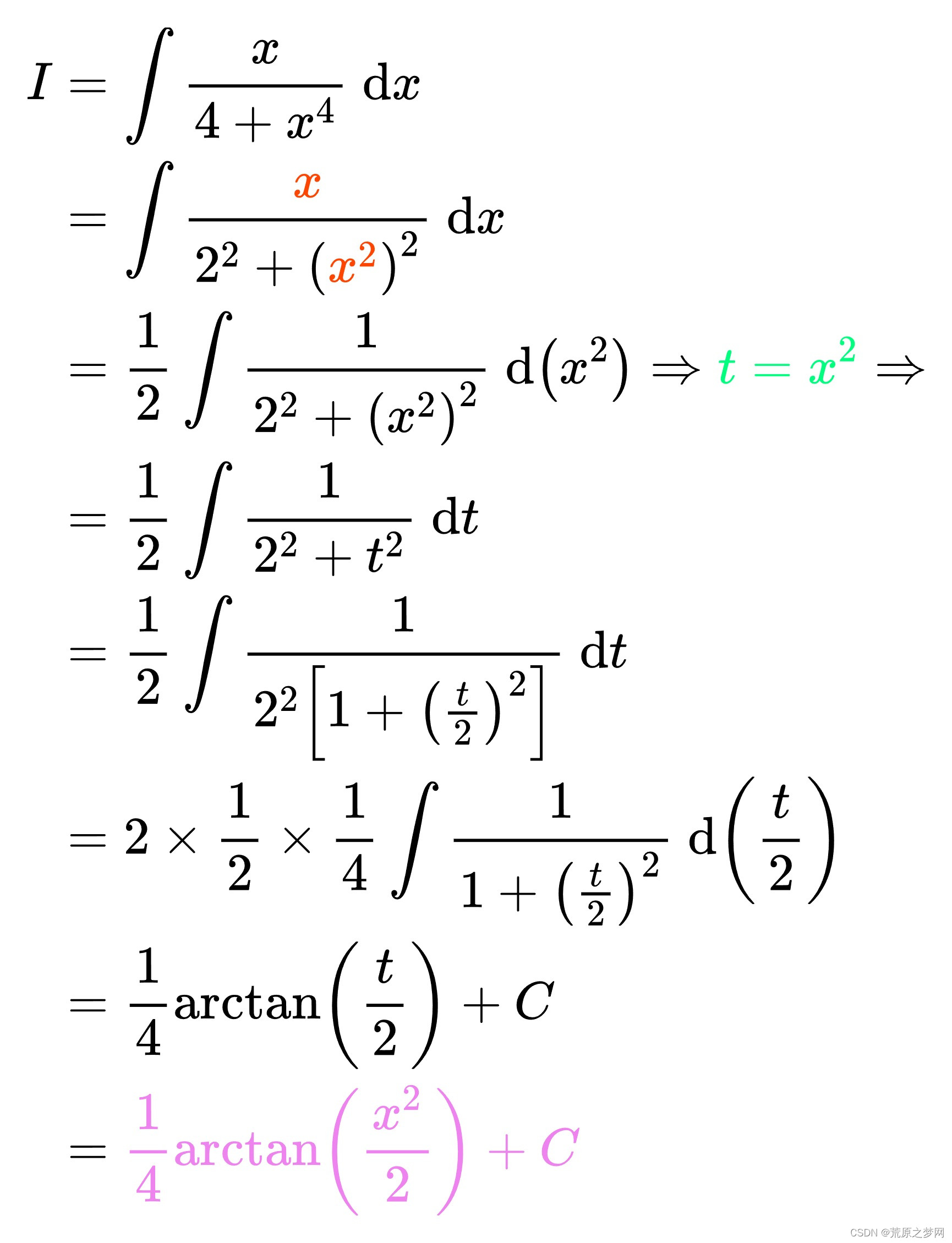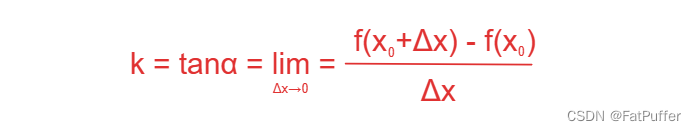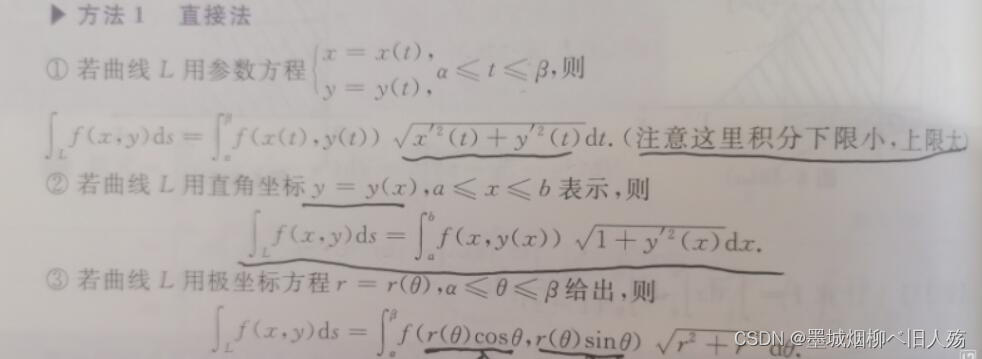arm
网络安全
保研
拍照
图书馆选座系统
小目标
客快物流大数据
cocos2dx-lua
相机参数
eureka
paas
文档管理系统
java-ee
校园二手交易系统
金仓数据库
初识SpringBoot
双指针
serverless
bypassav
kylin
高等数学
2024/4/11 17:27:52高等数学:圆周率的计算方法
文章目录 1 割圆术2 无穷级数2.1 拉马努金(Ramanujan)圆周率公式2.2 Chudnovsky圆周率公式2.3 BBP公式2.4 其他级数(1) 自然数倒数偶次方和(2) 泰勒展开(3) 无穷乘积 3 微积分4 概率学(Monte Carlo)5 连分数6 总结 本文将对圆周率 π \color{red}{\pi} π的计算方法作简单整理&…
函数的七大结论【总结,f(x),导数,积分】
上一部分对于函数的四大特性进行了讲解,这是属于中学数学的。
但是我们大学中学的是微积分,所以更加关注 导数 和 积分 考微积分:一定是给f’(x),然后研究它的微分(导数) 和 积分 f(x)、f’(x)、f(x)积分的…
【考研数学】高等数学第四模块——微分方程
文章目录 一、微分方程基本概念二、一阶微分方程的种类及解法2.1 可分离变量的微分方程2.2 齐次微分方程2.3 一阶齐次线性微分方程2.4 一阶非齐次线性微分方程2.5 伯努利方程2.6 全微分方程 三、可降阶的高阶微分方程四、高阶微分方程4.1 高阶线性微分方程4.1.1 基本概念4.1.2 …
高等数学:勾股定理证明方法
最著名的平面几何定理可能非勾股定理莫属。有意思的是,我们是从 3 3 3开始认识勾股定理的,勾三股四弦五, 3 2 4 2 5 2 3^{2}4^{2}5^{2} 324252 。三是什么?三在中国文化里具有特殊重要性,“道生一,一生二…
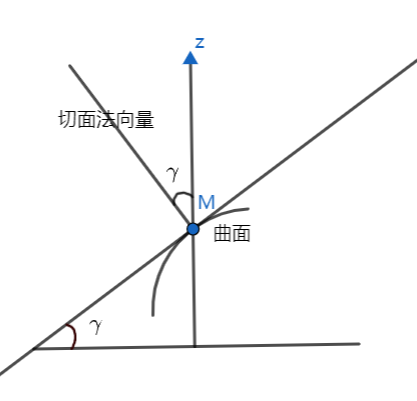
专题:曲面的切平面、法线
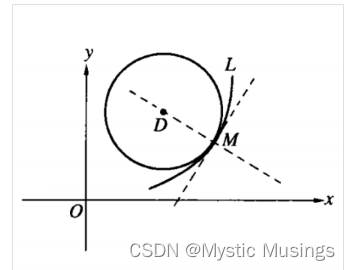
假设曲面方程为隐函数 F ( x , y , z ) 0 ,点 M ( x 0 , y 0 , z 0 ) 是其上一点 又在点 M 处任意引一条在曲面上的曲线,设该曲线参数方程为: { x φ ( t ) y ψ ( t ) z ω ( t ) ,且当 t t 0 时, x x 0 , y y…
高等数学:微积分(上)
文章目录 前言认清极限导数 前言
各位想要看完“作用量”系列的连载文章,不接触一点微积分知识怕是不行。我把之前零零碎碎写过的一些微积分的东西在此汇总,并配合“作用量”系列文章的要求进行了内容扩充。请你放一百个心,为了能让你有信心…
高等数学:坐标系变换式
文章目录 1、坐标系旋转公式2、坐标系平移公式3、复合变换 1、坐标系旋转公式
假设平面有一个点 P P P,在坐标系 X O Y XOY XOY 中的坐标为 ( x , y ) (x, y) (x,y),在坐标系 X ′ O ′ Y ′ XOY X′O′Y′ 中的坐标为 ( x ′ , y ′ ) (x, y) (x′…
060202体积弧长-定积分在几何学上的应用-定积分的应用
文章目录 2 体积2.1 旋转体的体积2.2 平行截截面面积已知的立体的体积2.3 例题 3 平面曲线的弧长2.1 直接坐标系2.2 参数方程2.3 极坐标系 结语 2 体积
2.1 旋转体的体积
情形①平面图形由 y f ( x ) , y 0 , x a , x b yf(x),y0,xa,xb yf(x),y0,xa,xb所围成,…
第二章(第二节):无穷小量和函数
1:无穷小量
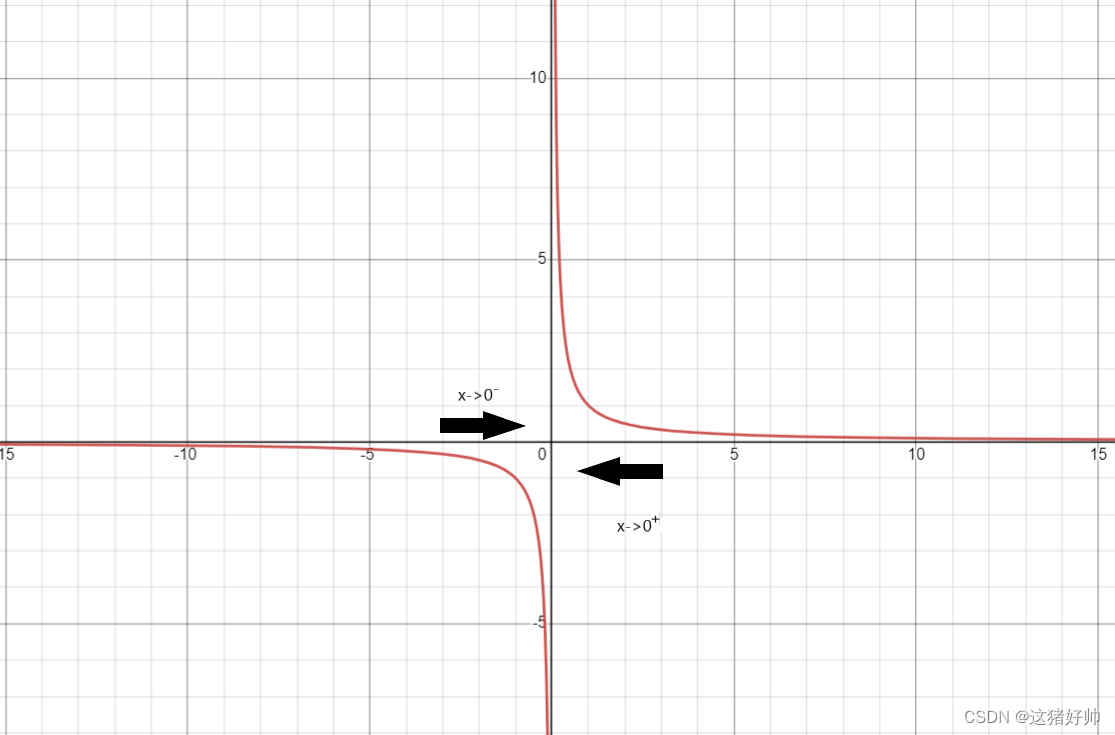
1.定义 若 lim f(x) = 0, 则称函数 f(x) 当 x → x0 时是无穷小量,简称:无穷小。 x→ x02.性质 定理1.有限多个无穷小量的代数和仍是无穷小量定理2.有限多个无穷小量的积也是无穷小量定理3.常数与无穷小量的积也是无穷小量定理4.有界变量与无穷小量的积是…
数学分析:函数序列及其一致收敛性
文章目录函数序列及其一致收敛性函数序列函数序列的一致收敛性函数序列一致收敛性的判别法一致收敛的函数序列的性质参考文献函数序列及其一致收敛性 \quad此前,我们已经可以用收敛数列(或收敛的数项级数)来表示或定义一个数,接下…
3.3 泰勒公式例题分析
例1 写出函数f(x)带有拉格朗日余项的n阶麦克劳林公式
我的答案:
一、信息
1.f(x)的表达式
2.目标求这个f(x)的n阶麦克劳林公式
二、分析
条件1:告诉我f(x)的表达式为我后续带入公式做准备
条件2:告诉我用什么公式和此次求解的方向
三…
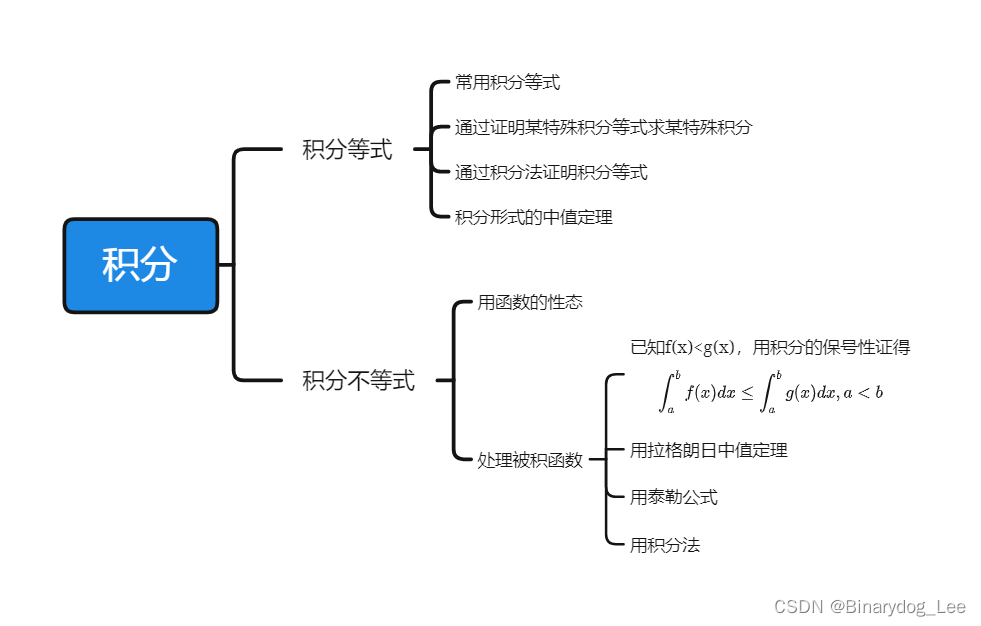
积分等式与积分不等式
参考资料:
B站 - 考研数学-积分不等式(所有方法全归纳)张宇基础和强化及习题册 积分等式
中值定理夹逼准则积分法 在这个专题中,有如下经验:
遇到 f ( x ) f(x) f(x)连续,应当想到变限积分 ∫ a x f ( t…
前言【高等数学教程1(单变量微积分)】
前言【高等数学教程1(单变量微积分)】
1. 什么是高等数学?
目前大部分高等院校教授的高等数学(advanced mathematics)课程内容主要是微积分(calculus)。
1.1 微积分的发明
微积分有两位主要的发明人,牛顿和莱布尼茨。 牛顿除了…
球面坐标系下的三重积分
涉及知识点
三重积分球面坐标系点火公式一些常见积分处理手法
球面坐标系定义
球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成
直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下: {xrsinφco…
线性代数基础【5】特征值和特征向量
第五章 特征值和特征向量
第一节、特征值和特征向量的基本概念
一、特征值和特征向量的理论背景
在一个多项式中,未知数的个数为任意多个,且每一项次数都是2的多项式称为二次型,二次型分为两种类型:即非标准二次型及标准二次型 注意:
①二次型X^T AX为非标准二次型的充分必…
AM@空间直角坐标系@数量积和向量积@向量的外积在物理学中的相关概念
文章目录 空间直角坐标系坐标面分向量坐标分解式余弦定理数量积的坐标表示公式 向量积向量积的坐标表示公式 向量的外积在物理学中的相关概念物理量ref 角速度和向量积量纲Base unit (measurement)Background🎈International System of Units🎈附 表达方…
【高等数学重点题型篇】——函数,极限与连续
本文仅用于个人学习记录,使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的,如有侵权,请联系删除! 文章目录 一、左右极限二、不定型极限的计算问题三、n项和或积的极限计算四、极限存在性问题…
高等数学基础篇(数二)之多元函数的基本概念
多元函数基本概念:
一、多元函数的极限
二、多元函数的连续性
三、偏导数
四、全微分 目录
一、多元函数的极限
二、多元函数的连续性
三、偏导数
1.偏导数的定义
2.二元函数偏导数的几何意义
3.高阶偏导数
四、全微分 补充:
一元函数极限连…
【高等数学】常见不定积分公式详细推导
常见积分公式注意事项!1 ∫cscxdxln∣cscx−cotx∣C\int cscxdxln|cscx-cotx|C∫cscxdxln∣cscx−cotx∣C2 ∫secxdxln∣secxtanx∣C\int secxdxln|secxtanx|C∫secxdxln∣secxtanx∣C3 ∫dxx2−a2ln∣xx2−a2∣C\int \frac{dx}{\sqrt{x^2-a^2}}ln|x\sqrt{x^2-a^2}|…
高等数学上册 第九章 多元函数微分法及其应用 知识点总结
多元函数微分法及其应用 ( 1 )多元函数的极限: 用“ ε − δ ”语言描述,二元函数的极限叫二重极限 二重极限存在: { 1 、 P ( x , y ) 一定要以任何方式趋于 ( x 0 , y 0 ) 时, f ( x , y ) 无限趋近于 A…
线性代数基础【4】线性方程组
第四章 线性方程组
一、线性方程组的基本概念与表达形式 二、线性方程组解的基本定理
定理1 设A为mXn矩阵,则
(1)齐次线性方程组AX0 只有零解的充分必要条件是r(A)n;
(2)齐次线性方程组AX0 有非零解(或有无数个解)的充分必要条件是r(A)<n
推论1 设A为n阶矩阵,则…
考研数学二复习笔记-高等数学-第一章 函数 极限 连续
反函数: 1.ysinx -->反函数为 y arcsinx x∈[- π 2 \frac{π}{2} 2π, π 2 \frac{π}{2} 2π] 推广: y π-arcsin x,x∈[ π 2 \frac{π}{2} 2π, 3 2 \frac{3}{2} 23π] 推算过程: ysinx sin(π-x) 因此反函数1. x arcsiny 2.π-xarcsiny 2.y cosx -->…
第十四届全国大学生数学竞赛决赛(非数类)游记+答案解析
2023/5/27 20:08:今天早上9:00~12:00考了数学竞赛国赛。广州是真的热啊!西安才17度,还下着小雨,到广州之后那个艳阳直接给我人干废了,去酒店的路上步行了20分钟真的要死了已经。
拿到卷子的我是崩溃的,用正…
最优化基础知识总结(1)
最优化基础知识总结(1) 最速下降方向:负梯度方向 梯度:沿各个坐标轴方向的偏导数组成的函数向量。 方向导数:梯度某一方向的单位向量。 黑塞矩阵:二阶偏导数,按列排列。第一列,为…
高等数学(第七版)同济大学 习题11-7 个人解答
高等数学(第七版)同济大学 习题11-7
函数作图软件:Mathematica 1.试对曲面Σ:zx2y2,x2y2≤1,Py2,Qx,Rz2验证斯托克斯公式.\begin{aligned}&1. \ 试对曲面\Sigma:zx^…
高等数学(第七版)同济大学 习题12-4 个人解答
高等数学(第七版)同济大学 习题12-4 1.求函数f(x)cosx的泰勒级数,并验证它在整个数轴上收敛于这函数.\begin{aligned}&1. \ 求函数f(x)cos\ x的泰勒级数,并验证它在整个数轴上收敛于这函数.&\end{aligned}1. 求函数f(x)…
线性代数基础【1】行列式
第一节 行列式的基本概念和性质
一、基本概念
①逆序
1,2和2,1是一对逆序
②逆序数
1,2,3,5,4的逆序数为1;1,3,2,5,4逆序数为4;
③行列式
④余子数和代数余子数
行列式挖掉一个数(例如aij),将原行列式去掉i行j列的行列式M,则M为余子数,代数余子数记为Aij,如果(ij)为偶数…
2.4 隐函数和参数方程的导数 相关变化率
思维导图: 学习目标:
了解基本概念:首先需要了解隐函数和参数方程的概念,以及它们与显式函数的区别。隐函数是指由两个或多个变量之间的方程定义的函数,而参数方程则是通过使用一个或多个参数来定义的函数。学习求导方…
高数笔记05:不定积分与定积分
图源:文心一言
时间比较紧张,仅导图~~🥝🥝
第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武忠祥 🐳目录 🐳目录 🐳不定积分 &#…
线性代数——(期末突击)矩阵(上)-概念篇(矩阵的定义、矩阵的运算、特殊矩阵、初等变换)
目录
矩阵的定义
矩阵的运算
相加
相乘
数乘
与单位阵相乘
矩阵的幂
转置
特殊矩阵
数量矩阵
对称矩阵
伴随矩阵
逆矩阵
初等变换 矩阵的定义
由个数排成的m行n列的数表,称为m行n列的矩阵,简称矩阵,记作: 简记为…
线性代数基础【2】矩阵
第二章 矩阵
第一节 矩阵的基本概念与特殊矩阵
一、基本概念
①矩阵
像如下图示的为矩阵,记为A(aij)m*n ②同型矩阵及矩阵相等
若A、B为如下两个矩阵 如果A和B的行数和列数相等,那么A和B为同型矩阵,且A和B的元素相等(即:aijbij),则称A和B相等
③伴随矩阵 设A为mn矩阵(如上…
第二章(第一节):数列与极限
1.数列及其极限
1.内容概述 极限理论是高等数学的基础,高等数学中的很多基本概念都是借助极限的方法来描述的,我们以数列为研究,引入极限的概念2.数列的通项公式 一个数列{an}的第n项,an与项数n的关系,如果可以用一个公式来表示,这个公式就叫做这个数列的通项公式。 1.数…
3.5 函数的极值与最大值和最小值
学习目标:
我要学习函数的极值、最大值和最小值,我会采取以下几个步骤: 理解基本概念:首先,我会理解函数的极值、最大值和最小值的概念。例如,我会学习函数在特定区间内的最高点和最低点,并且理…
高数笔记04:微分方程与多元函数微分学
图源:文心一言
时间比较紧张,仅导图~~🥝🥝
第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武忠祥 🦮思维导图 😶🌫️思维导图为整…
高等数学:微积分(下)
文章目录 微分积分结语 微分
导数说完了就可以说微分了。还是看图中过A点的切线,其与竖直虚线相交于C点。其中CD段的距离可以表示为 C D k ⋅ Δ x CD k \cdot \Delta x\\ CDk⋅Δx 这里的系数k是一个不为零的常数。原因很简单,假设这条切线与x轴的夹…
5.3 定积分的换元积分法和分部积分法
学习目标:
学习定积分的换元积分法和分部积分法,我会采取以下步骤: 熟悉基本概念和公式:首先,要对定积分、换元积分法和分部积分法有基本的理解,并掌握它们的基本公式和性质。 学习经典例题:找…
线性代数基础【6】二次型
第一节、二次型的基本概念及其标准型
一、基本概念
①二次型
含n个变量x1,x2,…,xn,且每项都是2次的齐次多项式
②标准二次型
只含有平方项不含交叉项的二次型称为标准二次型
③二次型的标准化
设f(X)X^TAX 为一个二次型,经过可逆的线性变换XPY(即P为可逆矩阵)把二次型…
第一章 函数 极限 连续(解题方法须背诵)
(一)求极限的常用方法
方法1 利用有理运算法则求极限
方法2 利用基本极限求极限
方法3 利用等价无穷小求极限
方法4 利用洛必达法则求极限
方法5 利用泰勒公式求极限
方法6 利用夹逼准则求极限
方法7 利用定积分的定义求极限
方法8 利用单调有界…
第二章(第二节):导数与微分
1.导数与微分
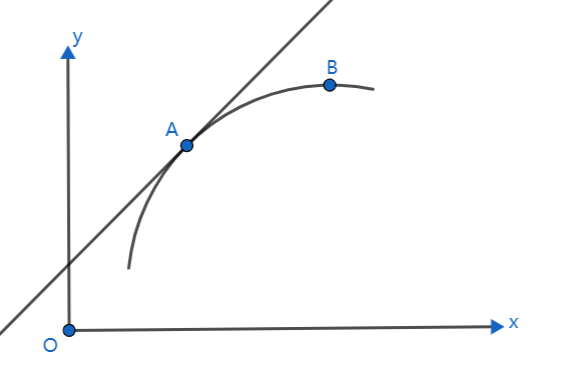
1.导数概念 设曲线 L 的方程 y=f(x),a ≤ x ≤ b,x0 ∈ (a, b),在曲线 L 上的点 M0(x0, y0) 附近任取一点 M(x0 + Δx, y0 + Δy),过 M0 与 M 作曲线的割线M~0~M,的斜率为:当 x→x0 时,点 M 沿着曲线 L 趋向 M0,与此同时,割线 M0M 趋向一个极限位置 M0T…
一阶线性微分方程计算公式推导
一阶线性微分方程的形式如下: y′p(x)yq(x)yp(x)yq(x)y′p(x)yq(x) 对于式子左侧,长得像下式,但不太一样 (uv)′u′vuv′(uv)uvuv(uv)′u′vuv′ y′⋅1y⋅p(x)y 1y p(x)y′⋅1y⋅p(x) 这里对应vvv看似得不到一个合适的,但是借助[…
0405习题总结-不定积分
文章目录1 不定积分的基本概念2 直接积分法-基本积分公式3 第一换元法-凑微分形式法4 第二类换元法5 分部积分求不定积分6 表格法积分7 有理函数求积分后记1 不定积分的基本概念
例1 f(x){x1,x≥012e−x12,x<0求∫f(x)dxf(x) \begin{cases} x1,\quad x\ge0\\ \frac{1}{2}e^…
常微分方程的解题思路
通解:独立常数的个数等于微分方程的阶数,独立常数的个数实际上就是 c 1 , c 2 , . . . , c n c_1,c_2,...,c_n c1,c2,...,cn是数目
所以补 C C C也是关键的一步,而且未必是 C C C,也可以是 ln C \ln C lnC之类的&…
高等数学上册 第二章 导数与微分 知识点总结
导数与微分
与导数概念的形成有密切关系的两个历史问题:
直线运动的速度切线问题
导数概念:极限存在>可导,极限就是导数
导函数:某一区间内所有点都可导,其导数值构成的新的函数
单侧导数:可导的充…
【高数:3 无穷小与无穷大】
【高数:3 无穷小与无穷大】 1 无穷小与无穷大2 极限运算法则3 极限存在原则4 趋于无穷小的比较 参考书籍:毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京:清华大学出版社,2022. 1 无穷小与无穷大
无穷大在sympy中用两个字母o表示无…
6.2 龙格—库塔法
学习目标:
学习龙格-库塔法的具体明确的学习目标可以有以下几点: 理解龙格-库塔法的基本思想和原理:我们应该了解龙格-库塔法的数值求解思想和数值误差的概念,包括截断误差和稳定性等基本概念,并且要熟悉龙格-库塔法的…
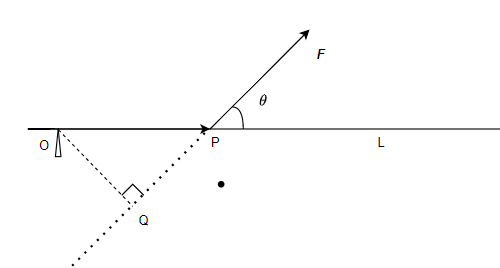
专题:平面、空间直线参数方程下的切线斜率问题
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。 如上图所示。 设 y f ( x ) , x φ ( t ) , y ψ ( t ) 当 t t 0 时, x x 0 , y y 0 ,即点 A 坐…
傅里叶级数系数的完整详细算法
傅里叶级数系数的完整详细算法
一、三角函数相关公式和定积分
在分析傅里叶级数之前,一定要先熟悉三角函数的相关公式,以及三角函数的积分。
1、两角和公式:
sin(αβ) sin(α) * cos(β) cos(α) * sin(β)
sin(α-β) sin(α) * co…
0504反常积分-定积分
文章目录1 无穷限的反常积分1.1 定义1.2 计算公式1.3 例题2 无界函数的反常积分2.1 定义2.2 计算公式2.3 例题结语1 无穷限的反常积分
1.1 定义
设函数f(x)在区间[a,∞)上连续,人去t>a,做定积分∫atf(x)dxf(x)在区间[a,\infty)上连续,人去t\gt a,做…
数学分析:换元积分法与分部积分法
8.2 换元积分法与分布积分法
一、换元积分法
定理 4:(第一类换元积分法) \quad设函数 f(x)f(x)f(x) 在区间 III 上有定义,φ(x)\varphi(x)φ(x) 在区间 JJJ 上可导,且 φ(J)⊂I\varphi(J) \subset Iφ(J)⊂I. 若不定…
0701微分方程的基本概念-微分方程
文章目录 1 基本概念2 例题结语 1 基本概念
例1 一曲线过点 ( 1 , 2 ) (1,2) (1,2),且在该曲线上任一点 M ( x , y ) M(x,y) M(x,y)处的切线斜率为 2 x 2x 2x,求曲线方程。 解:设曲线方程为 y f ( x ) , 则 d y d x 2 x ( 1 − 1 ) ∵ 曲线过点 ( 1 …
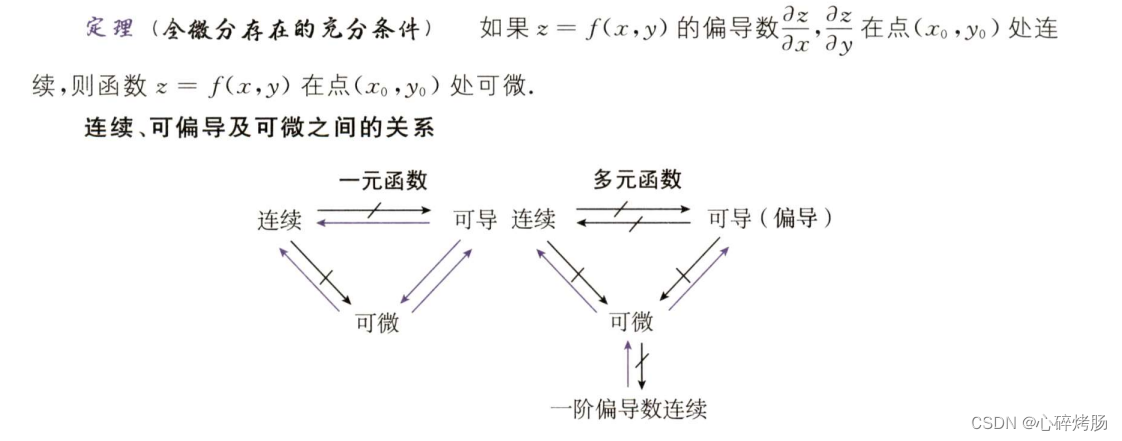
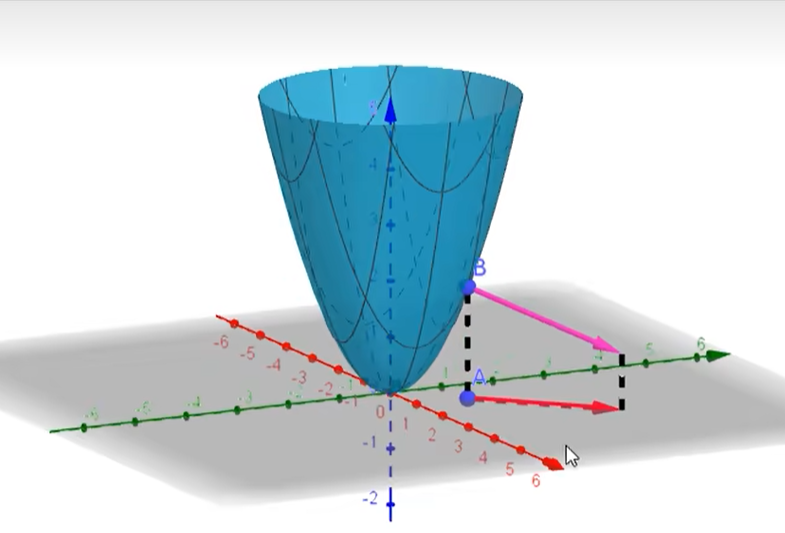
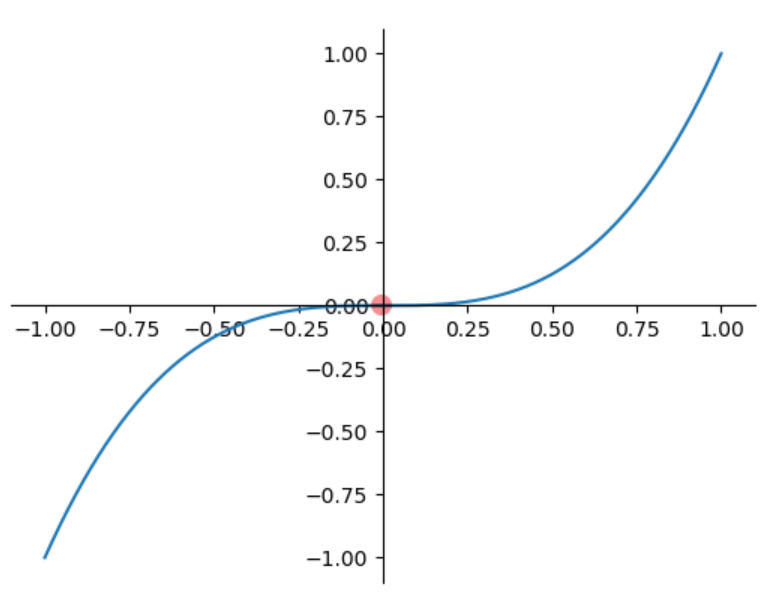
多元函数可导为什么不一定连续
多元函数可导是指x,yx,yx,y两个方向的偏导数∂z∂x\partial z \over \partial x∂x∂z 、∂z∂y\partial z \over \partial y∂y∂z 存在。 所以,多元函数可导只能说明动点(x,y0)(x,y_0)(x,y0)(或(x0,y)(x_0,y)(x0,y))沿x(…
0805曲面及其方程-向量代数与空间解析几何
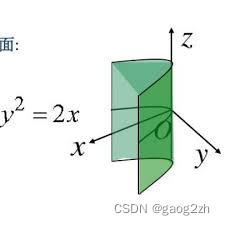
文章目录 1 曲面研究的基本问题2 旋转曲面3 柱面4 二次曲面4.1 定义4.2 研究方法4.3 九种二次曲面 结语 1 曲面研究的基本问题
曲面研究的两个基本问题:
已知一曲面作为点的几何轨迹时,建立这曲面的方程;已知x,y和z直接的一个方程时&#x…
考研数学二复习笔记-高等数学-第二章 一元函数微分学
1.导数和微分 求导
使用导数的定义 f ′ ( x ) lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 或者 f ′ ( x ) lim Δ x → 0 f ( x 0 Δ x ) − f ( x 0 ) Δ x f(x)\lim_{x \to{x0}}\frac{f(x)-f(x0)}{x-x0} 或者f(x)\lim_{Δx \to0}\frac{f(x0Δx)-f(x0)}{Δx} f…
高数笔记03:几何、物理应用
图源:文心一言
本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝
第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武…
0901多元函数的基本概念-多元函数微分法及其应用
文章目录 1 平面点集1.1 坐标平面1.2 平面点集1.3 邻域1.4 电与点集的关系1.5 聚点1.6 点集所属点的特征定义的平面点集 2 多元函数的概念2.1 定义2.2 值域2.3推广2.4 自然定义域2.5 二元函数的图形 3 多元函数的极限4 多元函数的连续性4.1 连续函数定义4.2 间断点定义4.3 多元…
AM@映射@函数@反函数@复合函数
文章目录 abstract直接定义函数的定义反函数定义复合函数定义 基于映射定义映射像原像定义域值域小结例满射单射👺双射映射的其他称呼 逆映射复合映射映射间可复合条件复合顺序 函数基于映射的函数相关定义函数函数的记法及其含义函数值 f ( x ) f(x) f(x)函数关系 …
线性代数基础【3】向量
第一节 向量的概念与运算
一、基本概念
①向量
②向量的模(长度)
③向量的单位化
④向量的三则运算
⑤向量的内积
二、向量运算的性质
(一)向量三则运算的性质
α β β αα (β γ) (α β) γk (α β) kα kβ(k l) α kα lα
(二)向量内积运…
人工智能所需高等数学知识大全(收藏版)
来源:投稿 作者:愤怒的可乐 编辑:学姐 不懂数学是学不好人工智能的,本系列文章就汇总了人工智能所需的数学知识。本文是高等数学篇。 另有线代篇和概率论篇
函数与极限
函数
yf(x) ,x是函数f的自变量,y是因变量
函…
0305函数的极值与最大值最小值-微分中值定理与导数的应用
文章目录1 极值1.1 定义1.2 求极值的一般方法2 最大值最小值问题2.1 求最值的一般步骤2.2 某个区间有一个驻点且该处是函数的极值点2.3 实际问题2.4 证明不等式后记1 极值
1.1 定义 设函数f(x)在点x0f(x)在点x_0f(x)在点x0的某邻域U(x0)U(x_0)U(x0)内有定义,如…
「高等数学」雅可比矩阵和黑塞矩阵的异同
「高等数学」雅可比矩阵和黑塞矩阵的异同
雅可比矩阵,Jacobi matrix 或者 Jacobian,是向量值函数( f : R n → R m f:\mathbb{R}^n \to \mathbb{R}^m f:Rn→Rm)的一阶偏导数按行排列所得的矩阵。
黑塞矩阵,又叫海森矩…
【高等数学】极限(上)(最全万字详解)
文章目录 1、数列的极限1.1、数列极限的定义1.2、为什么收敛数列极限是唯一的?1.3、为什么收敛数列是有界的?1.4、数列极限的保号性1.4.1、极限保数列值1.4.2、数列值保极限值 1.5、收敛数列与其子列之间的关系 2、函数极限概念2.1、函数极限的定义2.1.1…
高数笔记06:无穷级数
图源:文心一言
时间比较紧张,仅导图~~🥝🥝
第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武忠祥 🐳目录 🐳常数项级数 🐋概要 &…
高等数学上册 第十章 重积分 第十一章 曲线积分与曲面积分 知识点总结
重积分 二重积分计算法: 直角坐标下:化为二次积分 { 如果图形是 X Y 型,则都可以,但要考虑哪个计算不定积分方便 如果图形既不是 X 也不是 Y 型,则要拆分 极坐标下: ∬ f ( x , y ) d x d y ∬ f ( ρ cos…
高等数学(上)【基础学科、极限部分】
学习【高等数学(上)】6小时从0基础直追满绩!_哔哩哔哩_bilibili 高数基础
高等数学无非分为三个部分:极限、导数(微分)和积分——构成了微积分 高等数学学的就是 微积分,整体其实只是一个思想 …